2025
Abstract
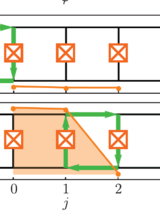
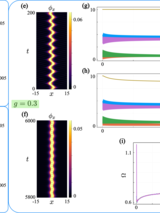
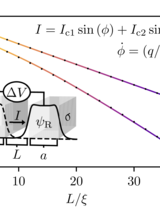
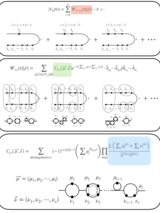
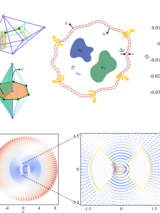
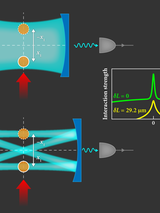
We investigate the long-time dynamics of the Sine-Gordon (SG) model under a class of perturbations whose quantum field theoretic analog — via bosonization — corresponds to the massive Schwinger model describing 1+1D relativistic QED of Dirac fermions. Classical SG solutions offer critical insight into non-perturbative effects in this quantum theory, but capturing their long-time behavior poses significant numerical challenges. To address this, we extend a coarse-graining method to spacetime using a dual-mesh construction based on the Minkowski-metric. We first validate the approach against the well-studied variant of the SG model describing magnetic fluxon dynamics in Josephson transmission lines (JTLs), where analytical and numerical benchmarks exist. We then apply the method to the Schwinger-inspired SG model and uncover long-lived bound states — “Schwinger atoms” — in which a soliton is trapped by a fixed central charge. In certain regimes, the system exhibits limit cycles that give rise to positronium-like states of oppositely charged solitons, while in others such formation is suppressed. Accessing such long-time solutions requires a rigorous implementation of outgoing boundary conditions on a finite computational domain that provide radiative dissipation to allow relaxation toward states that exist only in an infinite domain. Here we provide such a construction. Our results also suggest the possibility of analog quantum simulation of relativistic quantum field theories with JTLs. These results demonstrate the utility of spatio-temporal coarse-graining methodology for probing non-perturbative structure formation in non-linear field theories.
Abstract
We derive a mesoscopic theory of the Josephson junction from nonrelativistic scalar electrodynamics. Our theory reproduces the Josephson relations with the canonical current phase relation acquiring a weak second harmonic term, and it improves the standard lumped-element descriptions employed in circuit quantum electrodynamics by providing spatial resolution of the superconducting order parameter and electromagnetic field. By providing an ab initio derivation of the charge qubit Hamiltonian that relates traditionally free qubit parameters to geometric and material properties, we progress toward the quantum engineering of superconducting circuits at the subnanometer scale.
2024
Abstract
Many recent advancements in quantum computing leverage strong drives on nonlinear systems for state preparation, signal amplification, or gate operation. However, the interplay within such strongly driven system introduces multi-scale dynamics that affects the long-time behavior of the system in non-trivial ways that are very difficult to model. Therefore, the analysis of these systems often relies on effective Hamiltonian models that introduce additional nonlinear processes which approximate the long-time dynamics so that highly oscillatory terms may be ignored. However, the removal of such high frequency transitions can only be performed rigorously within a systematic framework of time-coarse graining, which is a fundamentally irreversible operation. This implies that standard approaches with unitary effective models cannot accurately capture the long-time behavior of strongly driven nonlinear quantum systems in general. We introduce a systematic perturbation theory for obtaining the complete non-unitary effective model of the time-coarse grained (TCG) dynamics of a driven quantum system to any order in the coupling strengths. We derive a closed-form analytical formula for both unitary and non-unitary contributions, in the form of an effective Hamiltonian and non-unitary (pseudo-)dissipators. Remarkably, even though the effective theory presumes unitary time evolution at the microscopic level, the time-coarse grained dynamics is found to follow a nonunitary time evolution in general. This occurs even when there is no open heat reservoir for the system to become entangled with or dissipate into. We demonstrate the effectiveness of the new method using several typical models of driven nonlinear systems in superconducting circuits, and show that it generalizes and improves on existing methods by providing more accurate results and explaining phenomena that have not been accounted for.
Abstract
Model order reduction encompasses mathematical techniques aimed at reducing the complexity of mathematical models in simulations while retaining the essential characteristics and behaviors of the original model. This is particularly useful in the context of large-scale dynamical systems, which can be computationally expensive to analyze and simulate. Here, we present a model order reduction technique to reduce the time complexity of open quantum systems, grounded in the principle of measurement-adapted coarse-graining. This method, governed by a coarse-graining time scale τ and the spectral band center ω0, organizes corrections to the lowestorder model which aligns with the RWA Hamiltonian in certain limits, and rigorously justifies the resulting effective quantum master equation (EQME). The focus on calculating to a high degree of accuracy only what can be resolved by the measurement introduces a principled regularization procedure to address singularities and generates low-stiffness models suitable for efficient long-time integration. Furthermore, the availability of the analytical form of the EQME parameters significantly boosts the interpretive capabilities of the method. As a demonstration, we derive the fourth-order EQME for a challenging problem related to the dynamics of a superconducting qubit under high-power dispersive readout in the presence of a continuum of dissipative waveguide modes. This derivation shows that the lowest-order terms align with previous results, while higher-order corrections suggest new phenomena.
Abstract
Although linear quantum amplification has proven essential to the processing of weak quantum signals, extracting higher-order quantum features such as correlations in principle demands nonlinear operations. However, nonlinear processing of quantum signals is often associated with non-idealities and excess noise, and absent a general framework to harness nonlinearity, such regimes are typically avoided. Here we present a framework to uncover general quantum signal processing principles of a broad class of bosonic quantum nonlinear processors (QNPs), inspired by a remarkably analogous paradigm in nature: the processing of environmental stimuli by nonlinear, noisy neural ensembles, to enable perception. Using a quantum-coherent description of a QNP monitoring a quantum signal source, we show that quantum nonlinearity can be harnessed to calculate higher-order features of an incident quantum signal, concentrating them into linearly-measurable observables, a transduction not possible using linear amplifiers. Secondly, QNPs provide coherent nonlinear control over quantum fluctuations including their own added noise, enabling noise suppression in an observable without suppressing transduced information, a paradigm that bears striking similarities to optimal neural codings that allow perception even under highly stochastic neural dynamics. Unlike the neural case, we show that QNP-engineered noise distributions can exhibit non-classical correlations, providing a new means to harness resources such as entanglement. Finally, we show that even simple QNPs in realistic measurement chains can provide enhancements of signal-to-noise ratio for practical tasks such as quantum state discrimination. Our work provides pathways to utilize nonlinear quantum systems as general computation devices, and enables a new paradigm for nonlinear quantum information processing.
Abstract
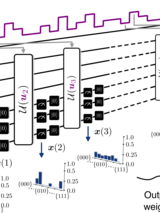
The practical implementation of many quantum algorithms known today is limited by the coherence time of the executing quantum hardware and quantum sampling noise. Here we present a machine learning algorithm, NISQRC, for qubit-based quantum systems that enables inference on temporal data over durations unconstrained by decoherence. NISQRC leverages mid-circuit measurements and deterministic reset operations to reduce circuit executions, while still maintaining an appropriate length persistent temporal memory in the quantum system, confirmed through the proposed Volterra Series analysis. This enables NISQRC to overcome not only limitations imposed by finite coherence, but also information scrambling in monitored circuits and sampling noise, problems that persist even in hypothetical fault-tolerant quantum computers that have yet to be realized. To validate our approach, we consider the channel equalization task to recover test signal symbols that are subject to a distorting channel. Through simulations and experiments on a 7-qubit quantum processor we demonstrate that NISQRC can recover arbitrarily long test signals, not limited by coherence time.
Abstract
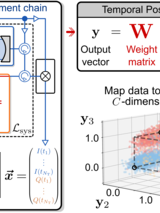
We develop and demonstrate a trainable temporal postprocessor (TPP) harnessing a simple but versatile machine learning algorithm to provide optimal processing of quantum measurement data subject to arbitrary noise processes for the readout of an arbitrary number of quantum states. We demonstrate the TPP on the essential task of qubit state readout, which has historically relied on temporal processing via matched filters in spite of their applicability for only specific noise conditions. Our results show that the TPP can reliably outperform standard filtering approaches under complex readout conditions, such as high-power readout. Using simulations of quantum measurement noise sources, we show that this advantage relies on the TPP’s ability to learn optimal linear filters that account for general quantum noise correlations in data, such as those due to quantum jumps, or correlated noise added by a phase-preserving quantum amplifier. Furthermore, we derive an exact analytic form for the optimal TPP weights: this positions the TPP as a linearly scaling generalization of matched filtering, valid for an arbitrary number of states under the most general readout noise conditions, all while preserving a training complexity that is essentially negligible in comparison with that of training neural networks for processing temporal quantum measurement data. The TPP can be autonomously and reliably trained on measurement data and requires only linear operations, making it ideal for field-programmable gate array implementations in circuit QED for real-time processing of measurement data from general quantum systems.
2023
Abstract
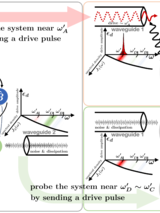
The accurate modeling of mode hybridization and calculation of radiative relaxation rates have been crucial to the design and optimization of superconducting quantum devices. In this work, we introduce a spectral theory for the electrohydrodynamics of superconductors that enables the extraction of the relaxation rates of excitations in a general three-dimensional distribution of superconducting bodies. Our approach addresses the long-standing problem of formulating a modal description of open systems that is both efficient and allows for second quantization of the radiative hybridized fields. This is achieved through the implementation of finite but transparent boundaries through which radiation can propagate into and out of the computational domain. The resulting spectral problem is defined within a coarse-grained formulation of the electrohydrodynamical equations that is suitable for the analysis of the non-equilibrium dynamics of multiscale superconducting quantum systems.
Abstract
The expressive capacity of physical systems employed for learning is limited by the unavoidable presence of noise in their extracted outputs. Though present in physical systems across both the classical and quantum regimes, the precise impact of noise on learning remains poorly understood. Focusing on supervised learning, we present a mathematical framework for evaluating the resolvable expressive capacity (REC) of general physical systems under finite sampling noise and provide a methodology for extracting its extrema, the eigentasks. Eigentasks are a native set of functions that a given physical system can approximate with minimal error. We show that the REC of a quantum system is limited by the fundamental theory of quantum measurement and obtain a tight upper bound for the REC of any finitely sampled physical system. We then provide empirical evidence that extracting low-noise eigentasks can lead to improved performance for machine learning tasks such as classification, displaying robustness to overfitting. We present analyses suggesting that correlations in the measured quantum system enhance learning capacity by reducing noise in eigentasks. The applicability of these results in practice is demonstrated with experiments on superconducting quantum processors. Our findings have broad implications for quantum machine learning and sensing applications.
Abstract
Coherent multimode instabilities are responsible for several phenomena of recent interest in semiconductor lasers, such as the generation of frequency combs and ultrashort pulses. These techonologies have proven disruptive in optical telecommunications and spectroscopy applications. While the standard Maxwell-Bloch equations encompass such complex lasing phenomena, their integration is computationally expensive and offers limited analytical insight. In this paper, we demonstrate an efficient spectral approach to the simulation of multimode instabilities via a quantitative analysis of the instability of single-frequency lasing in ring lasers, referred to as the Lorenz-Haken (LH) instability or the Risken-Nummedal-Graham-Haken (RNGH) instability in distinct parameter regimes . Our approach, referred to as CFTD, uses generally non-Hermitian Constant Flux modes to obtain projected Time Domain equations. CFTD provides excellent agreement with finite-difference integration of the Maxwell-Bloch equations across a wide range of parameters in regimes of non-stationary inversion, including frequency comb formation and spatiotemporal chaos. We also develop a modal linear stability analysis using CFTD to efficiently predict multimode instabilities in lasers. The combination of numerical accuracy, speedup, and semi-analytic insight across a variety of dynamical regimes make the CFTD approach ideal to analyze multimode instabilities in lasers, especially in more complex geometries or coupled laser arrays.
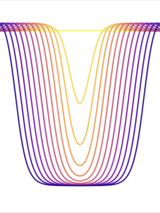
Abstract
Despite being largely limited to bulk phenomena, well-known theoretical models of superconductivity like the Bardeen–Cooper–Schrieffer and Ginzburg–Landau theories have played a key role in the development of superconducting quantum devices. In this letter, we present a hydrodynamic non-relativistic scalar electrodynamic theory capable of describing systems comprising superconducting materials of arbitrary shape and apply it to predict the existence of a negative (attractive) pressure between planar superconducting bodies. For conventional superconductors with London penetration depth λL ≈ 100 nm, the pressure reaches tens of N/mm2 at angstrom separations.
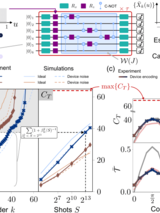
Abstract
The expressive capacity for learning with quantum systems is fundamentally limited by the quantum sampling noise incurred during measurement. While studies suggest that noise limits the resolvable capacity of quantum systems, its precise impact on learning remains an open question. We develop a framework for quantifying the expressive capacity of qubit-based systems from finite numbers of projective measurements, and calculate a tight bound on the expressive capacity and the corresponding accuracy limit that we compare to experiments on superconducting quantum processors. We uncover the native function set a finitely-sampled quantum system can approximate, called eigentasks. We then demonstrate how low-noise eigentasks improve performance for tasks such as classification in a way that is robust to noise and overfitting. We also present experimental and numerical analyses suggesting that entanglement enhances learning capacity by reducing noise in eigentasks. Our results are broadly relevant to quantum machine learning and sensing applications
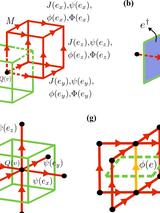
Abstract
Modeling the behavior of superconducting electronic circuits containing Josephson junctions is crucial for the design of superconducting information processors and devices. In this paper, we introduce DEC-QED, a computational approach for modeling the electrodynamics of superconducting electronic circuits containing Josephson junctions in arbitrary three-dimensional electromagnetic environments. DEC-QED captures the nonlinear response and induced currents in BCS superconductors and accurately captures phenomena such as the Meissner effect, flux quantization, and Josephson effects. Using a spatial coarse-graining formulation based on discrete exterior calculus (DEC), DEC-QED can accurately simulate transient and long-time dynamics in superconductors. The expression of the entire electrodynamic problem in terms of the gauge-invariant flux field and charges makes the resulting classical field theory suitable for second quantization.
2022
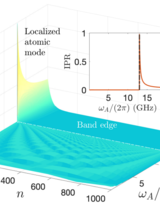
Abstract
We study the radiative properties -- the Lamb shift, Purcell decay rate and the spontaneous emission dynamics -- of an artificial atom coupled to a long, multimode cavity formed by an array of Josephson junctions. Introducing a tunable coupling element between the atom and the array, we demonstrate that such a system can exhibit a crossover from a perturbative to non-perturbative regime of light-matter interaction as one strengthens the coupling between the atom and the Josephson junction array (JJA). As a consequence, the concept of spontaneous emission as the occupation of the local atomic site being governed by a single complex-valued exponent breaks down. This breakdown, we show, can be interpreted in terms of formation of hybrid atom-resonator modes with radiative losses that are non-trivially related to the effective coupling between individual modes. We develop a singular function expansion approach for the description of the open quantum system dynamics in such a multimode non-perturbative regime. This modal framework generalizes the normal mode description of quantum fields in a finite volume, incorporating exact radiative losses and incident quantum noise at the delimiting surface. Our results are pertinent to recent experiments with Josephson atoms coupled to high impedance Josephson junction arrays.
2021
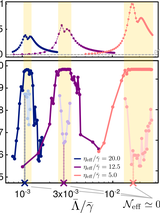
Abstract
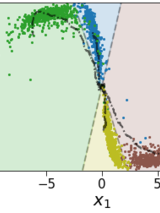
Abstract
2020
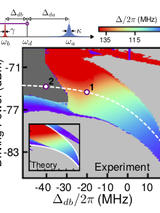
Abstract
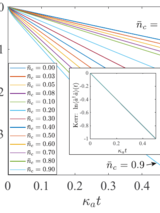
Abstract
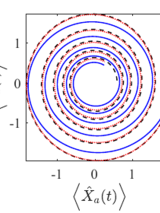
Abstract
2018
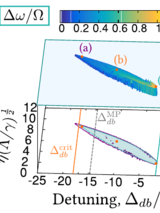
Abstract
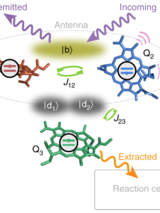
Abstract
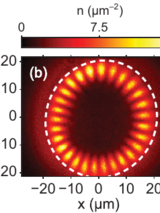
Abstract

Abstract