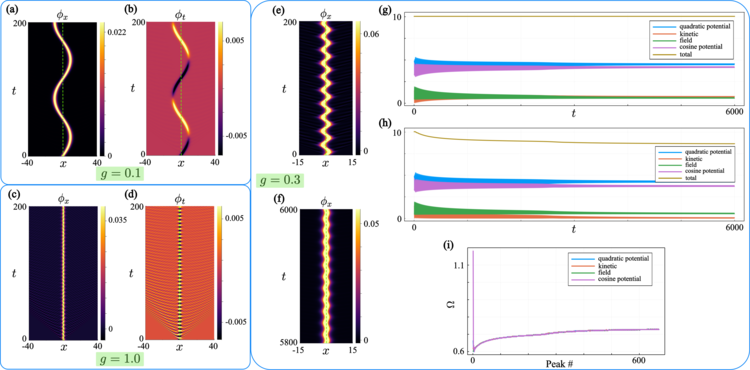
We investigate the long-time dynamics of the Sine-Gordon (SG) model under a class of perturbations whose quantum field theoretic analog — via bosonization — corresponds to the massive Schwinger model describing 1+1D relativistic QED of Dirac fermions. Classical SG solutions offer critical insight into non-perturbative effects in this quantum theory, but capturing their long-time behavior poses significant numerical challenges. To address this, we extend a coarse-graining method to spacetime using a dual-mesh construction based on the Minkowski-metric. We first validate the approach against the well-studied variant of the SG model describing magnetic fluxon dynamics in Josephson transmission lines (JTLs), where analytical and numerical benchmarks exist. We then apply the method to the Schwinger-inspired SG model and uncover long-lived bound states — “Schwinger atoms” — in which a soliton is trapped by a fixed central charge. In certain regimes, the system exhibits limit cycles that give rise to positronium-like states of oppositely charged solitons, while in others such formation is suppressed. Accessing such long-time solutions requires a rigorous implementation of outgoing boundary conditions on a finite computational domain that provide radiative dissipation to allow relaxation toward states that exist only in an infinite domain. Here we provide such a construction. Our results also suggest the possibility of analog quantum simulation of relativistic quantum field theories with JTLs. These results demonstrate the utility of spatio-temporal coarse-graining methodology for probing non-perturbative structure formation in non-linear field theories.